前几天在朋友圈看到一个有趣的问题,引发了很多朋友的讨论:
“有三扇门,其中一扇后面是大奖,另外两扇后面是小奖品。你先选一扇门,之后知道答案的人会打开剩下两扇门里有小奖品的那扇,再问你要不要换去选另一扇没开的门?”
这其实是一个非常经典、甚至有点反直觉的概率问题,它被称为“蒙提霍尔问题”(Monty Hall Problem)。很多人第一反应是:既然只剩下两扇门,一扇有奖一扇没奖,那换不换的概率都是50%对50%,换不换都一样。
如果你也这么想,那么恭喜你,你掉进了大多数人都会掉进的思维陷阱里!

问题到底出在哪?
直觉告诉我们,当一扇错误的门被排除后,剩下的两扇门机会均等。但我们忽略了一个至关重要的信息:主持人的行为不是随机的。他知道哪扇门后面有大奖,并且他永远不会打开那扇有奖的门。他总是有意地打开一扇后面是“山羊”(小奖品)的门。
这个“刻意”的行为,改变了整个事件的概率分布。
让我们来一步步分解
假设你一开始选择了门1。你选中大奖的概率是 1/3,而大奖在另外两扇门(门2或门3)后面的概率是 2/3。
现在,关键的一步来了。主持人会打开一扇有山羊的门。
-
情况一:如果你一开始就选对了(概率为 1/3) 你选了门1,大奖就在门1后面。那么主持人可以在门2和门3里随便打开一扇(因为后面都是山羊)。他打开后问你换不换,如果你选择换,你必定会输。
-
情况二:如果你一开始选错了(概率为 2/3) 你选了门1,但大奖其实在另外两扇门后面。
- 如果大奖在门2,主持人必须打开门3。他问你换不换,你从门1换到门2,你就赢了。
- 如果大奖在门3,主持人必须打开门2。他问你换不换,你从门1换到门3,你就赢了。
看到了吗?在你最初选择错误的 2/3 的可能性中,只要你选择换,你总是会赢!
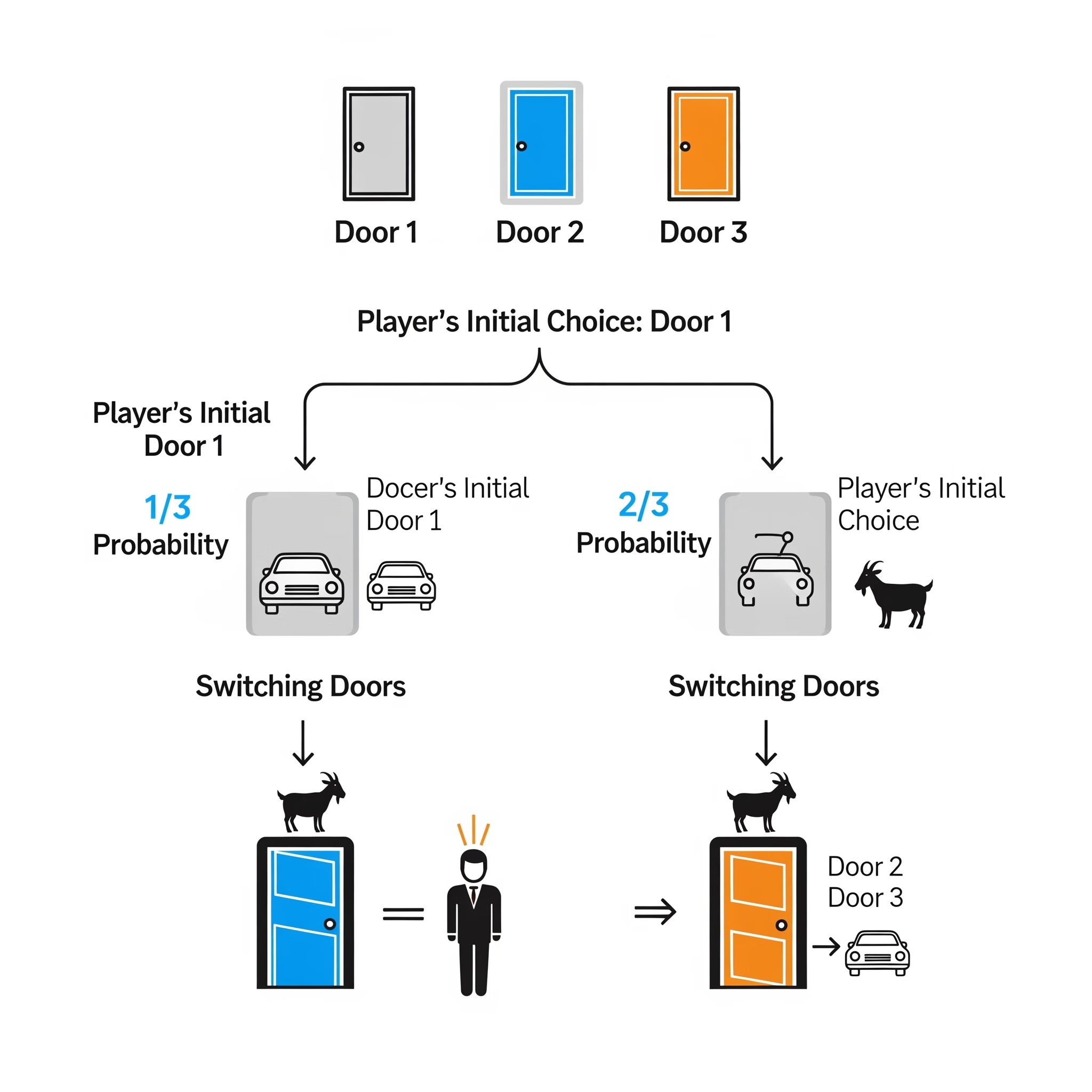
结论:果断换!
所以,我们来总结一下概率:
- 坚持不换:你赢的唯一机会就是你一开始就选对了,这个概率是 1/3。
- 选择交换:你赢的机会,来自于你一开始选错了,这个概率是 2/3。
换句话说,通过交换选择,你将赢得大奖的概率从 1/3 提升到了 2/3。这是一个巨大的优势!
这个问题的反直觉之处在于,我们很难摆脱“剩下两个选项,概率各一半”的惯性思维。但主持人的介入,提供了一个强大的信息——他帮你排除了一个错误答案,这个信息极大地压缩了你最初选择范围内的“不确定性”,并将那 2/3 的“错误概率”全部集中到了剩下那扇未被开启的门上。
生活中的启示
蒙提霍尔问题不仅仅是一个有趣的数学谜题,它也告诉我们,在做决策时,要仔细考虑所有已知信息,特别是那些看起来不太起眼,但实际上改变了整个格局的“隐藏条件”。有时候,我们最初的选择可能基于不完整的信息,而当新的、有价值的信息出现时,勇敢地改变策略,可能才是通往成功的更优路径。
所以,下次再遇到类似的选择,不妨多想一步。问问自己:那个“主持人”是谁?他给了我什么新的信息?
那么,现在轮到你了,如果是你,你会选择换吗?在评论区告诉我你的想法吧!

Comments